Mesura el tamany de la Terra

Et proposo el següent repte: que tu mateix mesuris la circumferència de la Terra.
Sí, tu! I no et preocupis, no necessitaràs donar la volta al món amb una cinta mètrica 🤭
➤ Una mica d'història: Eratòstenes i la seva èpica gesta de mesurar la Terra!
Imagina això: som a l'antiga Grècia, fa més de 2000 anys. No hi ha Google Maps, ni satèl·lits, ni res d'això. Però hi ha un tipus anomenat Eratòstenes que decideix averiguar quina grandària té la Terra. I ho fa amb una precisió impressionant! Com ho va aconseguir? Doncs, agafa't fort perquè aquesta història és increïble.
Qui era Eratòstenes?

Eratòstenes era un geni. Va néixer a Cirene (el que ara és Líbia) i era un expert en tot: matemàtiques, astronomia, poesia, filosofia... fins i tot va ser el cap de la Biblioteca d'Alexandria! Sí, la mateixa biblioteca legendaria.
L'enginy d'Eratòstenes
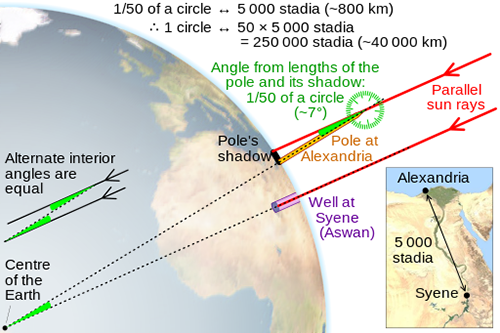
Eratòstenes va fer el càlcul d'una manera senzilla i enginyosa. Aquí t'ho explico pas a pas:
-
Solstici d'estiu a Siena (Assuan)
Sabia que a Siena, una ciutat al sud d'Egipte, al migdia del solstici d'estiu, el sol era just a la vertical. És a dir, sense ombres! Els objectes es veien com si haguessin desaparegut.
-
Mesurant ombres a Alexandria
El mateix dia i a la mateixa hora, Eratòstenes estava a Alexandria, que és al nord de Siena. Aquí, les coses eren diferents: hi havia ombres. Va mesurar l'altura d'un obelisc i la seva ombra i va calcular que l'angle era de 7.2 graus.
-
L'angle màgic
Aquest angle de 7.2 graus era com una pista de detectius. Perquè si el sol està a la vertical en un lloc i fa un angle de 7.2 graus en un altre, significa que aquests 7.2 graus són una fracció del cercle complet de la Terra (360 graus).
-
La distància entre les ciutats
Eratòstenes sabia que la distància entre Siena i Alexandria era d'uns 5000 estadis (una unitat de mesura de l'època).
-
Calculant la circumferència
Utilitzant una senzilla regla de tres, va deduir que si 7.2 graus eren 5000 estadis, llavors 360 graus serien 50 vegades aquesta distància. Va fer els càlculs i voilà! La circumferència de la Terra seria de 250000 estadis.
Convertint això a quilòmetres, resulta que estava bastant a prop de la xifra real que coneixem avui: uns 40000 quilòmetres. Res malament per no tenir una calculadora, eh!
➤ Ara et toca a tu!
T'agradaria seguir els passos d'Eratòstenes i mesurar el diàmetre de la Terra tu mateix? Aquí et deixo una guia perquè ho puguis fer de manera senzilla!
Dia i hora
21 de juny a les 12 del migdia hora solar
Materials
- Sol (per poder mesurar l'ombra)
- Pal
- Cinta mètrica
- Paper i llapis per apuntar
- Calculadora
- Internet
- Nivell (opcional)
Pas a pas
-
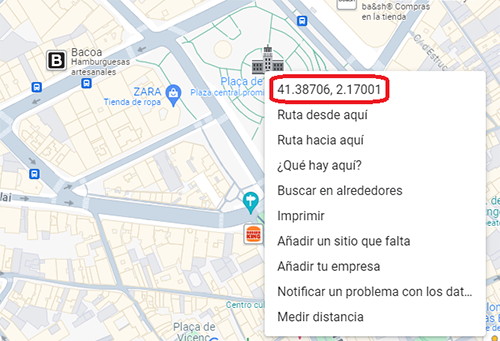
Longitud i latitud
Cerca la longitud i latitud del lloc on faràs les mesures. Per fer-ho pots utilitzar Google Maps:
- Cerca la localització on faràs les mesures
- Fes clic amb el botó dret a la teva localització
- Apunta al teu paper la longitud i latitud
-
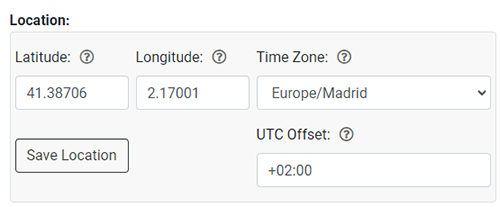
Hora de rellotge que correspon al migdia solar
Actualment la majoria dels fusos horaris no corresponen a l'hora solar, per la qual cosa has de buscar l'hora que correspongui al migdia solar. Per fer-ho pots utilitzar el web del Global Monitoring Laboratory:
- Apunta en Location: la teva latitud i longitud
- Apunta en Date: el 21 de juny
- Apunta al teu paper l'hora solar (Solar Noon)
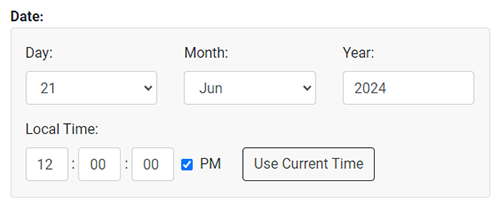

Ara ja saps a quina hora prendre les mesures. En el meu cas hauré de fer-ho el més proper possible a les 13:53:08
-
Distància des de la teva ubicació al tròpic de Càncer
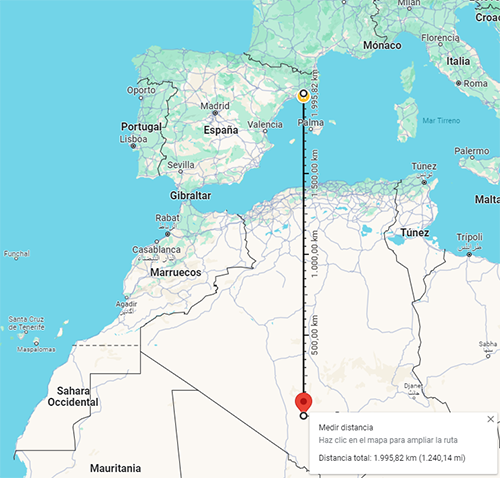
Pots trobar la distància entre la teva ubicació i el tròpic de Càncer utilitzant Google Maps:
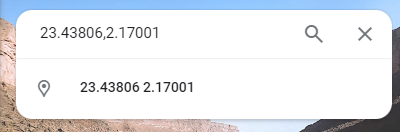
- Cerca la ubicació del tròpic de Càncer a Google Maps, per fer-ho has de buscar la longitud del tròpic de Càncer que és 23.43806 i la latitud de la teva ubicació (en el meu cas 2.17001)
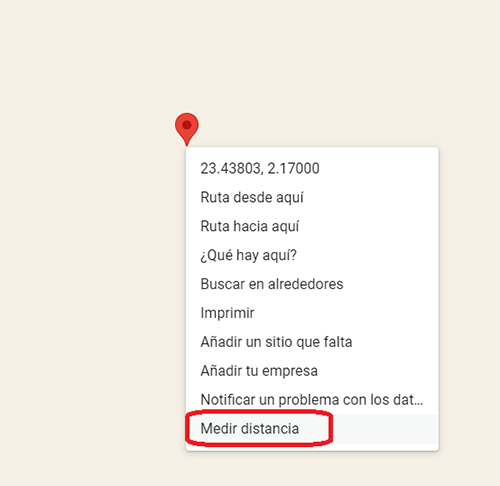
- Fes clic amb el botó dret per mesurar distàncies
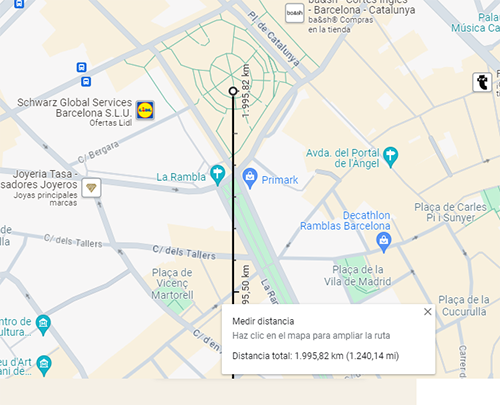
- Cerca la teva ubicació i fes clic per mesurar
- Anota en el teu paper la distància (en el meu cas 1995,82 km)
-
Mesurant ombres
Ara sí, ha arribat el moment de mesurar la grandària de la Terra.
- La mesura l'has de fer el 21 de juny al migdia solar (en el meu cas a les 13:53)
- Pren el teu pal i col·loca'l en un lloc on doni el sol per poder mesurar la seva ombra.
- Verifica que el terra és totalment horitzontal, per això pots utilitzar un nivell
- Assegura't que el pal està completament vertical
- A l'hora del migdia solar mesura l'ombra que projecta el teu pal al terra
- Mesura l'altura del pal
-
Calcula l'angle de l'ombra
Utilitza les mesures de l'ombra i l'altura del pal per calcular l'angle de l'ombra. Pots utilitzar la fórmula trigonomètrica:
tan(angle) = longitud de l'ombra / altura de l'objecte.- Pren la calculadora
- Divideix la longitud de l'ombra per l'altura de l'objecte
- angle = arctan(longitud de l'ombra / altura de l'objecte)
- Anota el resultat en el teu paper
-
Calcula la circumferència de la Terra
Utilitza la proporció d'Eratòstenes:
circumferència = (360 graus / diferència d'angles) * distància entre els llocs.
-
Troba el diàmetre de la Terra
Divideix la circumferència obtinguda entre π (pi ≈ 3.14159) per obtenir el diàmetre de la Terra:
diàmetre = circumferència / π.
-
Possibles errors
La circumferència de la Terra és de 40075 km i el seu diàmetre d'uns 12756 km.
Quins valors t'han sortit a tu? És molt possible que els teus valors siguin diferents als reals, però haurien de ser aproximats.
És molt fàcil cometre petits errors que provoquen una desviació en el càlcul, perquè et facis una idea, un sol mil·límetre de diferència en la longitud de l'ombra dóna lloc a una diferència de més de 100 km.
També hem de tenir en compte que la Terra no és completament rodona, que la mesura depèn del nivell del mar sobre el qual estiguis, que hi ha aixafament de la Terra...
La cosa important és que t'ha de donar un valor aproximadament i que tu has pogut calcular el diàmetre de la Terra utilitzant un pal. 👏👏👏
I això és tot! Amb aquests senzills passos, podràs mesurar el diàmetre del nostre planeta, tal com va fer Eratòstenes fa més de 2000 anys. Bona sort i diverteix-te experimentant!